Perseverance Pays
In plain terms, compound interest is simply the result of reinvesting your returns each year, rather than paying them out. Every year that goes by, you receive investment returns not only on your capital invested but also on your previous investment returns (i.e. you get interest on your interest).
So how much difference does it make? Let us look at some examples;
Example 1 – Investing a Lump Sum
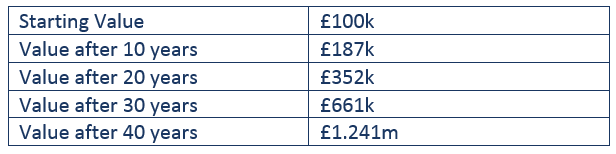
Let us assume that we invest the sum of £100,000 in a stock-market based portfolio which we will assume grows at a steady 6.5% per annum. In reality we know that the returns from such a portfolio will be anything but steady, with markets rising some years and falling the next, but nonetheless this exercise will help demonstrate the point.
Every 10 years the cumulative total return is approximately 87%.
- For the first 10 years, the increase on your investment is therefore £87,000.
- For the next 10 years however, the increase on your investment is £167,000 (£352k minus £187k), which is almost twice the amount made in the first 10 years.
- If we remain invested over 40 years, the increase over the last 10 years is an impressive £580,000
Example 2 – Saving for the future
James is aged 24 years old and is contemplating setting up an investment plan to save for the future. He is hoping to retire at aged 65 years old and asks BRI for some advice.
(For simplicity we will again assume the funds are invested in a stock-market based portfolio with annual investment returns of 6.5% per annum)
Option A
BRI’s advice is to start saving as soon as you can. From the age of 25, start saving the sum of £250 per month for the next 40 years into an ISA which will grow tax free.
Option B
James hopes that his salary will rise in the future and is attracted to the idea of spending what he earns now and saving later. His alternative plan is to delay saving until he is 35 years old, when he believes he will be better placed to afford it and make up the difference and lost time by saving twice as much but over slightly less time, i.e. £500 per month for a 30-year period.
Which option is best for James?
Option a) will cost James a total of £120,000 whilst option b) will cost a total of £180,000.
However, despite costing less, option a) will produce a bigger lump sum of £574,000 compared with
the £556,00 produced by Option b)
Conclusion
The advancement of technology over the last few decades has had a dramatic impact upon the speed at which stock markets now move, with computer algorithms driving huge trading volumes in the blink of an eye. The short-term traders and their strategies seen in the late 80’s and 90’s are no longer able to rely upon their gut instincts to outwit fellow traders, as the computers are faster and devoid of emotion. A longer-term strategy is therefore key to obtain longer term returns.



